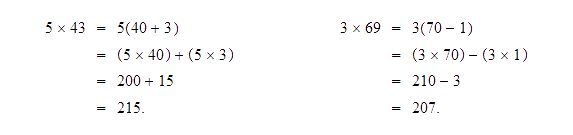::Colección Conocimientos Fundamentales::

Módulo I El campo de los ... El campo de los números reales Introducción Los números enteros Suma de números enteros Ejercicios Resta de números enteros Ejercicios Multiplicación de números enteros Ejercicios El orden de los números enteros Ejercicios Factores primos y máximo común divisor Ejercicios Los números reales Intervalos Leyes de los exponentes	Indice > Módulo I: El campo de los números reales> Multiplicación de números enteros Los números enteros Multiplicación de números enteros Desde la primaria sabemos cómo multiplicar números positivos; veamos ahora una interpretación geométrica de la multiplicación que nos permitirá entender mejor la multiplicación con números negativos. Ejemplos Multiplicar 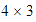$4\times 3$ . Solución: Marcamos el 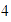en el eje horizontal, y en el eje vertical marcamos 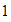el y el 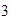. Unimos con una recta el 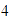del eje horizontal con el 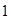del eje vertical. Por el 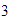del eje vertical, trazamos una recta paralela a la anterior y observamos el punto donde corta al eje horizontal. El punto donde corta es el resultado de la multiplicación: 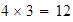$4\times 3=12$ . 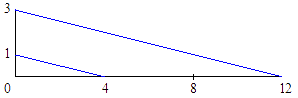Interpretación geométrica de 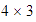$4\times 3$ . La razón de lo anterior es que los triángulos formados son semejantes, así que si la altura del mayor es 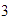veces la altura del menor, entonces la base del mayor es 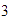veces la base del menor, es decir, 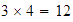$3\times 4=12$ . Hagamos la misma construcción cuando uno de los factores es negativo: Multiplicar 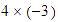. 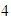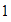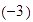Solución: Marcamos el en el eje horizontal, y en el eje vertical marcamos el y el $\left( -3\right)$ . 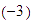Observa que $\left( -3\right)$ está en la parte inferior del eje. Unimos con una recta el 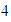del eje horizontal con el 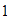del eje vertical. Por el 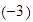$\left( -3\right)$ del eje vertical, trazamos una recta paralela a la anterior y observamos el punto donde corta al eje horizontal. 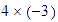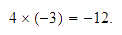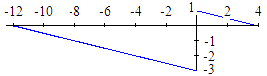El punto donde corta es el resultado de la multiplicación , así, Interpretación geométrica de 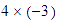. Multiplicar 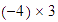. 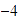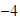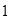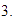Solución: Marcamos en el eje horizontal (observa que está en la parte izquierda del eje), y en el eje vertical marcamos el y el Unimos con una recta el 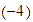$\left( -4\right)$ del eje horizontal con el 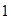del eje vertical. 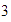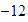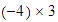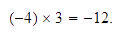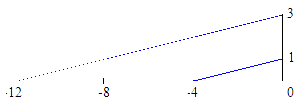Por el del eje vertical, trazamos una recta paralela a la anterior y observamos el punto donde corta al eje horizontal; así, el punto , donde corta, es el resultado de la multiplicación, : Interpretación geométrica de 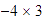$-4\times 3$ . Veamos ahora el caso en el que ambos factores son negativos: Multiplicar 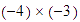. Solución: Marcamos 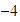en el eje horizontal, y en el eje vertical marcamos el 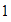y el . 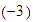Unimos con una recta el 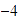del eje horizontal con el 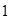del eje vertical. Por e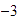l del eje vertical, trazamos una recta paralela a la anterior y observamos el punto donde corta al eje horizontal. 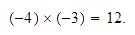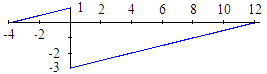El punto donde corta es el resultado de la multiplicación, que en este caso es: Interpretación geométrica de 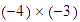. Notación para la multiplicación En aritmética, usualmente usamos el signo 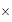$\times$ para denotar la multiplicación, pero en álgebra hay veces que podemos suprimirlo para simplificar la notación. 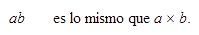Cuando utilizamos letras para representar números, simplemente las ponemos una junto a otra para denotar el producto, así Cuando el signo de multiplicación está junto a un paréntesis, podemos suprimirlo: Leyes de los signos de la multiplicación Los cuatro ejemplos anteriores ejemplifican las leyes de los signos: El producto de dos números del mismo signo es positivo. El producto de dos números de signo contrario es negativo. 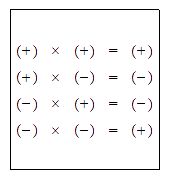Podemos recordar estas reglas con el siguiente cuadro: Ejemplos Multiplicar 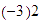$\left( -3\right) 2$ . 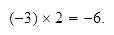Solución: Multiplicar 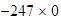$-247\times 0$ . Solución: Recuerda que el producto de cero por cualquier número es cero. 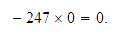Así Multiplicar 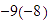. 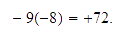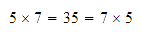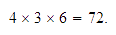Solución: Al multiplicar dos números, no importa el orden en que lo hacemos, de ahí la famosa frase ``El orden de los factores no altera el producto'' Y para multiplicar más de dos números, debemos agrupar dos de ellos, multiplicarlos y multiplicar el resultado por el resto, por ejemplo: así, podemos escribir simplemente Por otro lado, cuando tenemos una suma y un producto, debemos tener cuidado, ya que no es lo mismo efectuar primero el producto y después la suma, que hacerlo en el otro orden, por ejemplo: 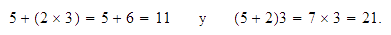Por eso es necesario establecer de manera inequívoca qué significa 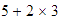$5+2\times 3$ . La regla que se sigue es: Más adelante veremos con más detalle este tipo de expresiones. Así, 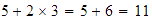$5+2\times 3=5+6=11$ , aunque es preferible usar paréntesis. 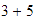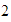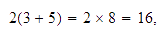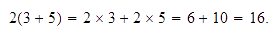Cuando tenemos una expresión como para poder efectuar la multiplicación, primero debemos saber el resultado de la suma , para después poder multiplicarlo por , así: sin embargo, también podríamos haberlo hecho de otra manera: multiplicar por 2 cada uno de los números que están en el paréntesis y después sumar los resultados: Que estas dos maneras de efectuar esta operación nos lleven al mismo resultado se le conoce como propiedad distributiva. Ejemplos Podemos ejemplificar lo anterior con peras y manzanas para entenderlo mejor. Si tenemos dos bolsas y en cada una hay 3 peras y 5 manzanas, ¿cuántas frutas tenemos? Primer razonamiento: En cada bolsa hay 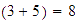frutas, así que tenemos 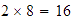$2\times 8=16$ frutas. Segundo razonamiento: Tenemos 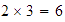$2\times 3=6$ peras y 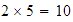$2\times 5=10$ manzanas, así que tenemos 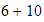frutas. 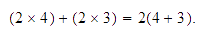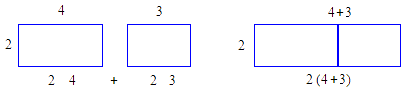También podemos ejemplificarla geométricamente de la siguiente manera Propiedad distributiva Podemos utilizar la ley distributiva para hacer las siguientes operaciones: Propiedades del producto de números enteros A continuación enunciamos las propiedades del producto de números enteros que hemos ejemplificado. Propiedad de cerradura: Si y son números enteros, entonces es un número entero. Propiedad conmutativa: Si y son números enteros, entonces . Propiedad asociativa: Si , y son números enteros, entonces . Existencia del neutro multiplicativo: El número satisface la igualdad $a\times 1=a$ para cualquier número entero . 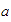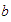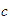La siguiente propiedad relaciona la suma y el producto y se llama propiedad distributiva de los números enteros: Si , y son números enteros, entonces . 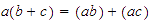[ Índice del módulo]

2006 © D.R. Universidad Nacional Autónoma de México. Programa de Conocimientos Fundamentales. Hecho en México. [ Derechos de autor y autorizaciones ]